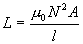1.1

Introduction:

According to history books, Galileo simultaneously dropped two balls of dissimilar mass from the tower of Pisa in Italy (this was before it started leaning, and became unsafe to ascend).  He observed that both balls hit the ground at the same moment, implying that both balls fell (accelerated) at the same rate.  In the 1970s, Apollo astronauts repeated this experiment on the surface of the Moon, using a hammer and a feather, and all those watching TV on Earth, observed the same result.

Why is this simple experiment considered so important that NASA would add a feather to the Apollo mission manifest, and schedule time during a Moon walk to repeat what Galileo did nearly 500 years ago?  The answer is both very simple, and at the same time, very profound.  The implications of this experiment apply to both conventional Newtonian kinetics, and to the more modern electrodynamic reformulation of gravity and inertial mass as understood from the relativistic perspective.

When considering the nature of mass, most contemporary science concentrates on what mass "is".  However, while this is certainly important, the thrust of this paper is phenomenological.  Therefore we shall concentrate of what mass "does", and use the knowledge of what mass "is" in a purely supporting role.

1.2

Force and gravity:

Force is defined in terms of the acceleration it causes in mass, as shown in Eq. 1

Where:

Since the Galileo experiment demonstrates that dissimilar masses fall (accelerate) at exactly the same rate (and assuming Eq. 1 is correct), we must conclude that the force causing acceleration (gravity) scales proportionately with mass, as shown in Eq. 2.

Where:

In the era of Galileo, the phenomenological basis for this result was a complete mystery.  Even Newton, while formalizing the result (F=Ma), was unable to explain why this result should be true.  The answer to "why " had to wait until science had a better understanding of what mass is composed of.

2.1.1

Composition and nature of mass:

The knowledge required to understand mass was discovered during the last half of the 19th century and the first half of the 20th century.  Thanks to J.J. Thomson (electron), Ernest Rutherford (atomic nuclei), and James Chadwick (neutron), the internal picture of the atom was completed in 1932.  In this modern picture, we have electrons moving in orbitals, around a compact nucleus composed of protons and neutrons.  At first glance these discoveries do not seem to explain the nature of mass.  However, when coupled with electrodynamics (Maxwell), all of the prerequisite pieces needed to understand mass are in place.

As we shall see, from this hand full of theories and observations, a rational, scientifically consistent explanation of mass can be synthesized.

2.1.2

Mass, two phenomena:

The first step to understanding mass is to realize that mass is actually two independent yet interrelated phenomena, consisting of inertial mass, and gravitational mass.  We are justified in this assertion by the fact that inertial mass interactions remain constant, while gravitational mass interactions very depending on location.  In other words, a constant force produces a constant acceleration in mass X (ignoring relativistic effects) regardless of location, while gravitational acceleration in mass X varies depending on location (Earth, Moon, Mars, etc.).  This assertion is also implied by dimensional analysis of Eq.2 (1.2 above), as shown in Eq. 3.

Where:

Conventional physics teaches inertial and gravitational interactions as part of mechanics (Newtonian kinetics).  Since this perspective is extrinsic (how it happens), rather than intrinsic (why it happens), its only natural to cancel the two "M"s out (in the right side of Eq. 3), and speak exclusively in terms of "the acceleration of gravity".  From this (mechanical) view point, gravity (Earth standard) is an acceleration of 9.8 meters per second squared.  However this view point obscures the true nature of gravity.  Gravity causes acceleration in mass.  Ergo, gravity is a force.  Furthermore, as Eq. 2 clearly demonstrates, the force is proportional to mass.  Therefore, gravity (Earth standard) is a force of 9.8 Newtons per Kilogram, NOT an acceleration of 9.8 meters per second squared.  In other words, the definition of gravity is "force per unit mass", and we can NOT cancel the two "M"s out of Eq. 3, because one "M" represents the "per Kilogram" that gravity is acting upon, while the other "M" represents the mass that is being accelerated (Eq. 1).  Or stated another way, inertial mass exists, independent of the force casing the acceleration, while gravitational mass exists only in the presence of a gravitational field.

One further indication of the duality of mass is implied by Eq. 4

Where:

Eq. 4 is reformulation of the standard Poynting vector equation, obtained by changing the electromagnetic wave from a traveling configuration, to a standing (rotating) configuration.  In making this change, the equation is transformed from describing the power per unit area of a electromagnetic wave, to describing mass.  Note that two vectors are required to rotate in 3 physical dimensions ("E" & "H") in order to create the effect called mass.  Again, we see duality in the phenomenological basis of mass.

Normally, we associate the E vector with electric phenomena such as capacitance, and the H vector with magnetic phenomena such as inductance.  However, these two vectors ("E" & "H"), and the twin phenomena they engender (magnetic induction and dielectric polarization), can also be used to gain a deeper, more precise insight into the dual effects of inertia and gravity, embodied in the concept called mass.

2.1.3

Subatomic mass:

Particle physics assigns a mass value to the electron, proton, and neutron.  This mass value can be interpreted in several ways.  Under Einstein's mass/energy equivalence, this mass value represents the quantity of energy required to "create" the particle, or the quantity of energy released when the particle is "annihilated".  And as in conventional kinetics, the mass value relates the rate of acceleration to the accelerating force acting on the particle.  However, in the case of the proton and electron, we can NOT use this assigned mass value to determine gravitational interaction.

Electrogravitic theory asserts that gravitational force arises as a result of unbalanced opposing forces within an electric dipole, caused by a non-uniform induced (BxV) electric field (see companion paper entitled Electrogravitics - Parts 1 & 2).  Neither the proton nor electron are dipoles, so while they will interact with the electrogravitic field, that interaction will NOT scale with the assigned mass value.  Because the charge of the proton and electron are equal and opposite, under the influence of the electrogravitic field, the two particles will accelerate in opposite directions.  Furthermore, since their (inertial) mass values are dissimilar, their rates of acceleration will be dissimilar, with the proton accelerating slower than the electron.  In the case of a neutron, inertial mass and gravitational mass do scale proportionally, since the neutron is a degenerate form of hydrogen, and therefore a dipole (see companion paper entitled The Unified Field - Part 1).

This brings us to the central issue of inertial mass.  If as I assert in my companion paper entitled "Inductive Momentum", inertial mass has as its root cause, magnetic induction, then how are we to reconcile the difference in electron and proton mass, when both particles have the same (though opposite) electric charge?  If inertial mass is caused by magnetic induction, we can rephrase the question (above) as follows:

Why is the electromagnetic inductance of a moving proton different than the electromagnetic inductance of a moving electron, when both particles have the same magnitude of electric charge?

The answer is found in the mathematical definition of an inductor.  The inductance of an air core solenoid is proportional to the core permeability, number of turns squared, core cross sectional area, and inversely proportional to solenoid length.  These relationships are shown in Eq. 5.

Where:

In a traditional inductor, the current encloses the magnetic flux.  But in the case of a moving electrically charged particle, the magnetic flux encloses the current (particle).  However, the dynamics are analogous.  In particular, just as solenoid inductance is proportional to the core cross sectional area, so too is the inductance of an electrically charged moving particle, proportional to the cross sectional area enclosed by the flux loop surrounding the particle.  After all, a larger flux loop threads a larger number of Dirac sea dipoles, requiring more energy to create correlation, or dipole alignment (see companion paper entitled Electrodynamic Structure of Space - Part 1).  The proton is larger than the electron (based on scattering experiments), and therefore the proton flux loop cross sectional area is also larger, thereby creating a larger inductance, and requiring a greater investment of energy for any given delta V, which of course particle physics interprets as greater inertial mass, or greater resistance to changes in velocity.

The mass value ratio between the proton and electron is approximately 1800:1.  One might naively expect the difference in observed particle diameters to be proportional to the square root of this ratio.  However, the situation is just a bit more complicated.  Remember that subatomic particle diameters are determined by scattering experiments, NOT by direct measurement.  Furthermore, the results obtained from scattering experiments are greatly influenced by particle interaction velocities.  Therefore, in many respects determining subatomic particle diameter is akin to determining planetary diameter for a gas giant.  Both are dependent on preconditions, set by the experimenter.  Collision energy of scattering interaction in the case of particle diameters, and minimum atmospheric pressure in the case of gas giant planetary diameters.

A further complication arises from the fact that space itself breaks down in the vicinity of charged subatomic particles, in effect surrounding each "bare" charged particle with a cloud of polarized Dirac sea dipoles, and thereby modifying the particles effective diameter.  This condition is, in many respects, analogous to the chemistry of ions in aqueous solution, where each ion is surrounded by a cloud of polarized water molecules.

A mass ratio of 1800:1 between the proton and electron implies an effective (bare charge + dipole cloud) diameter ratio of 42.426:1.

2.2.1

Inertial mass:

Macroscopic Inertial mass results from the combined electromagnetic induction of the electrically charged subatomic particles that are its constituent components.  This assertion rests upon several well tested observational facts.

1. An electric current is composed of electric charges, moving in a correlated manner.  i.e. all moving in the same overall direction.
2. ALL electric currents, irrespective of their nature, posses inductive properties.
3. Mass is composed of electrically charge particles, and therefore mass in motion IS an electric current.
4. Kinetic energy (energy of inertial mass in motion) and inductive energy (energy of charge in motion) have equivalent mathematical forms.
5. Moving collinearly with mass reduces its kinetic energy to zero, and equivalently, moving collinearly with electric charge reduces its magnetic field to zero.

See companion paper entitled "Inductive Momentum" for an in-depth treatment of inertial mass.

2.2.2

Gravitational mass:

Macroscopic gravitational attraction results from the combined imbalance of attractive and repulsive forces within the dipoles (proton/electron pairs) that are the constituent components of mass 1, when subjected to the induced (BxV) nonlinear electrogravitic field, generated by mass 2.  This assertion rests upon two sets of well tested observational facts.

 Mass as a gravitational field receiver

1. Within an atom, the segregation of protons (within the nucleus) and electrons (in an extended cloud) IS an electric dipole structure.
2. ALL electric dipoles polarize in the presence of ANY electric field, irrespective of dipole type, or electric field source.
3. In a non-uniform electric field, dipole polarization results in a net attractive force, with the force vector aligned to the electric field vector.

Mass as a gravitational field generator

1. Electric charge in motion produces a magnetic field.
2. Within an atom, individual electron motion within an orbital IS electric charge in motion.
3. Since electrons moving in orbitals are discrete charges, the magenetic field generated by an electron MUST also be discrete, attached to, and moving coincident with the electron.
4. Moving magnetic fields produce (induce) electric fields with a vector direction at right angles to both magnetic vector and velocity vector (BxV).
5. Two electrons moving in opposite directions, have opposite velocity vectors AND opposite magnetic field vectors, thereby generating identical electric (BxV) field vectors.  Therefore ALL BxV (induced electric fields) generated by electron motion within an atom have identical body centered vectors, and constitute a coherent non-uniform induced electric field.

In contrast to inertial mass, which exists even in a universe containing a single atom, gravitational mass requires the interaction of AT LEAST two atoms.

See companion paper entitled "Electrogravitics - Parts 1 & 2" for an in-depth treatment of gravitational mass.

2.2.3

Electric charge, two phenomena:

Electric charge participates in two distinct, yet interrelated classes of phenomena.  Dielectric phenomena, and inductive phenomena.  Today, in the modern age of computers and GPS satellites, its easy to forget that electromagnetic is really a compound word, composed of "electric" and "magnetic".  Just as mass has the dual characteristics of inertial and gravitational interactions, electric charge has the dual characteristics of dielectric and inductive interactions, and as shown in (2.1.1, 2.1.2, 2.1.3, 2.2.1, and 2.2.2), this symmetry of duality between mass and electric charge is no mere accident of chance.  It is the dual nature of electric charge interactions that gives rise to the dual nature of mass interactions.

There is one further symmetry between mass interactions and electric charge interactions, this is in fact the asymmetry between interaction types within each class.  Just as a single atom possesses inertial (kinetic) energy of motion, so too does a single electric charge posses magnetic (inductive) energy of motion.  However, just as gravitational interactions require two separate masses, so too does a dielectric interaction require two separate electric charges.  Here we see the asymmetry of electric charge interactions, mirrored in the macroscopic world of mass interactions they engender.

It is relatively easy to envision inertial mass as arising from magnetic induction, however gravitational mass is a more complicated affair, involving as it does, both a generator mass to produce the field, and a receiver mass affected by the field.  Is gravitation inductive or capacitive?  An argument could be made for both.  However, from the perspective of Galileo, dropping his balls from the tower of Pisa, it is mass as affected by the gravitational field that he witnessed.  Furthermore, as we have seen (1.2, 2.1.2, 2.2.2), it is the dielectric response of matter to the electrogravitic field, that gives rise to the force we call gravity.  Therefore, we are justified in calling gravitational attraction a dielectric effect, just as the asymmetry discussed in the preceding paragraph would imply.

3.1

Summary:

It is the twin characteristics (inductance and capacitance), embodied in electric charge interactions, that give rise to the twin characteristics (inertia and gravity) embodied in the effect locus we call mass.  This may seem an odd way to state the situation, however it is a cruel trick of semantics, arising from simian evolution, that cause the human mind to think of mass as an object, rather than a collection effects.  Therefore, to gain a deeper understanding of what mass is, we must concentrate on what mass does.  In other words (literally), we must transform the noun into a verb...

End

Galileo's Falling Balls