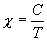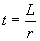3.1.1

Introduction:

In part 3 of this paper, we shall examine population inversions as they apply to electromagnets.  In particular, we shall discover that when viewed from the perspective of inverted populations, many devices reported as exhibiting phenomena or behavior, inconsistent with the second law of thermodynamics, are in fact, fully compliant with the second law of thermodynamics.

3.1.2

Paramagnetic materials:

Any material with un-paired electron spins will exhibit magnetic properties to a greater or lesser extent.  These un-paired electrons will spin align with the applied magnetic field.  In paramagnetic materials, the spin alignment disappears when the magnetic field is removed.  Materials that are easily polarized produce a greater paramagnetic response.  In thermodynamic terms, the paramagnetic properties of un-paired electrons represent separate degrees of freedom (dimensions in phase space) in addition to the normal degrees of freedom (vibration and movement) possessed by all materials.

Further, unlike atomic or molecular vibration/movement which exhibit strong coupling between dimensions in phase space (degrees of freedom), electron spin alignment is (in most cases) only weakly coupled to other dimensions of phase space.  For this reason, it is appropriate to consider paramagnetic materials as consisting of two separate populations (electron spins, and bulk vibration/movement) interconnected through a large thermal resistance.  Therefore, in many situations, each population will posses separate numerical values for entropy, energy, and temperature.

In the presence of a magnetic field, the rules of quantum electrodynamics require the un-paired electron spins be either aligned, or anti-aligned to the magnetic field vector (two dimensions in phase space).  Therefore, un-paired electron spins in paramagnetic materials represent an excellent material for constructing an inverted population boiler (2.1.4, 2.2.1, 2.2.4).

3.1.4

The inductor:

An inductor consists of an insulated wire, wrapped around a paramagnetic material, generally called the core.  Inductors exhibit the curious behavior of opposing any change in the flow of current through the insulated wire.  This electrical behavior is well understood by most scientists and engineers.  However, it seems that few scientists or engineers have ever bothered to consider the thermodynamic consequences of this behavior as it applies to the paramagnetic material comprising the core of the inductor.  Figure 2a shows an inductor, connected to a battery, through a switch.  When the switch is closed, an electric current starts to flow through the inductor, increasing linearly over time as shown in figure 2b.

Consider the population of un-paired electron spins in the paramagnetic core of the inductor, at the instants just before, and just after the switch is closed.

Before the switch is closed, there is no un-paired electron spin alignment, and therefore the un-paired electron spins have nearly limitless dimensions in phase space (degrees of freedom), AND the un-paired electron spin population is in thermal equilibrium with the bulk population.

After the switch is closed, phase space collapses to just 2 dimensions, because the un-paired electron spins must be either be aligned or anti-aligned to the applied magnetic field (3.1.2), AND since the paramagnetic polarization at this instant is zero (origin point in figure 2b), it follows that 50% are spin aligned, and 50% are anti-spin aligned.  Therefore, the temperature of the un-paired electron spin population is infinite (2.1.4), and obviously no longer in thermal equilibrium with the bulk population (heat flows from spin population into bulk population).

Next, as the current flowing through the inductor to rises, so does the magnetic field, thereby increasing paramagnetic polarization.  Anti-aligned electron spins are flipping into alignment with the magnetic field, and since entropy is declining as energy flows into the magnetic field (the battery is doing work on the inductor), Eq. 2b (part 2) implies the temperature of the electron spin population is now negative (hotter than infinity), AND declining (2.1.4 figure 1).  The situation is analogous to compressing a gas, where heat flows out of the hot gas, and into the container walls, except our "magnetic gas" is an inverted population (2.2.1, 2.2.4).

3.1.5

Inductive collapse:

Referring to figures 2a, and 2b (above), when the switch is opened current flow can not cease instantly.  The energy stored as un-paired electron spin alignments in the paramagnetic core must be removed (or dissipated) from the inductor before current can stop flowing.  The extreme case is represented by opening the switch, thereby causing an interruption of current flow, and results in an electrical arc across the switch contacts.

Consider the population of un-paired electron spins in the paramagnetic core of the inductor at the instants just before and after the switch is opened.

Before the switch was opened, current flow was rising (the battery was doing work on the inductor), un-paired electron spin alignment was increasing, electron spin temperature was negative and declining (inverted population), and heat was flowing out of the electron spin population, and into the bulk population (3.1.3).

After the switch is opened, the inductor must now do work on the rest of the electrical circuit in order to dissipate the energy stored in the magnetic field, supported by the un-paired electron spin alignments in the paramagnetic core.  However the un-paired electron spins can not spontaneously depolarize without gaining back the heat lost during alignment.  And since the energy contained in the inductor is being dissipated very quickly (by the arc), heat lost during alignment must now flow back into the un-paired electron spins very quickly as well.  The ONLY available avenue for the un-paired electron spin population to achieve rapid heat inflow, is for it's temperature to drop BELOW the temperature of the bulk population.  The situation is analogous to the explosive decompression of a gas, except of course our "magnetic gas" is an inverted population.

3.2.1

The magneto-thermodynamic engine cycle:

The magneto-thermodynamic engine cycle consists of three steps:

3.2.2

Theory of operation:

The magneto-thermodynamic cycle theory of operation assumes the following two conditions.

Step 1 (isothermal magnetization) shifts the un-paired electron spin population of the inductor core into an inverted population state (2.1.4, 2.2.1, 3.1.4).  During this step, as un-paired electron spins align with the applied magnetic field, the entropy of the population declines, and heat flows out of the un-paired electron spin population, and into the bulk material population (3.1.2).

Step 2 (adiabatic demagnetization) causes a rapid decline in the temperature of the un-paired electron spin population (3.1.5).  During this decline in temperature, the un-paired electron spin population momentarily dips below the Curie transition temperature (3.1.3), thereby causing a momentary rise in total magnetic flux as ferromagnetic spin coupling forces contribute to overall un-paired electron spin alignment.  This momentary flux increase represents an additional increment of electromagnetic energy (beyond the energy stored in the inductor during step 1), available to the driven circuit.  Therefore the electromagnetic energy derived from the inductor during step 2, is greater than the electromagnetic energy stored in the inductor during step 1.

Step 3 (thermal equalization) Allows sufficient time for the heat deficient (caused by step 2), to be replenished from the ambient environment.

As a practical consequence of the two conditions (listed above), the magneto-thermodynamic heat engine will operate from ambient heat sources, without requiring a lower temperature condenser to dump waste heat.  In other words, the magneto-thermodynamic heat engine is a "perpetuam mobile of the second type", and satisfies ALL requirements of James C. Maxwell's Daemon, as he envisioned it.

Next, we shall cover each step in detail.

3.2.3

Step 1, Isothermal magnetization:

In figure 2a (above) the rate of change in current flow is set by the ratio of electric potential (voltage) to inductance as shown in Eq. 6.

Where:

The rate of change in current flow can be made arbitrarily small, by making the ratio of electric potential to inductance small as well.

Since the degree of un-paired electron spin polarization is directly dependent on the magnitude of current flow through the inductor.  It follows that a small rate of change in current flow will yield an equally small rate of change in un-paired electron spin polarization, and this will result in a small rate of heat outflow (into the bulk material population), and therefore a small temperature rise across the thermal resistance separating the un-paired electron spin population from the bulk material population (3.1.2, 3.1.4), thereby causing the smallest possible decline in magnetic susceptibility of the paramagnetic core of the inductor (3.1.3).

Strictly speaking step one is NOT isothermal.  However by proper circuit design and choice of paramagnetic core material, the decline of magnetic susceptibility in the core of the inductor can be minimized, which is the ideal condition for this step.

This step represents the compression stroke of our engine.

3.2.4

Step 2, Adiabatic demagnetization:

The time required for inductive collapse is set by the ratio of inductance to driven circuit impedance as shown by Eq 7.

Where:

The length of time required for inductive collapse can be made arbitrarily short, by making the driven circuit impedance very large.

The purpose of this step is to force the temperature of the un-paired electron spin population to fall below the Curie transition temperature (3.1.3, 3.1.5, 3.2.2), and thereby cause the magnetic susceptibility of the core to become infinite (onset of ferromagnetic behavior).  The ideal condition is met when the rate of change in the magnetic field of the inductor never drops to zero.  If the un-paired electron spin population temperature become too cold, the core will momentarily "freeze" in the ferromagnetic state, thereby causing the rate of change in the magnetic field to become zero.

During this step, the heat inflow to the un-paired electron spin population from the bulk material population is greater than the heat outflow during step 1 (3.2.3).  The reason being that heat inflow must overcome both the electron spin coupling forces caused by passage through Curie transition, as well as the regular paramagnetic polarization.  Conversely, the electrical energy delivered to the driven circuit by the inductor during this step, is larger than the electrical energy stored in the inductor during step 1.

In effect, step two has converted quantity of thermal energy into electrical energy.

Strictly speaking step two is NOT adiabatic.  However, by proper circuit design and choice of paramagnetic core materials, the rise in magnetic susceptibility during this step can be made sufficiently large.

This step represents the power stroke of our engine.

3.2.5

Step 3, Thermal equalization:

As the name implies, the purpose of this step is to allow the electron spin population and the bulk material population to once more, achieve thermal equilibrium with the ambient environment.  While in the strict sense of the magneto-thermodynamic cycle, this step is not required, it's inclusion greatly simplifies circuit design.

This step represents the intake stroke of our engine.

Further, NO exhaust stroke is required, since our engine utilizes an inverted population of un-paired electron spins, as it's "working fluid" (2.2.4).

3.3.1

Summary:

The fringes of scientific research are literally teeming with reports of inductive kickback devices that exhibit anti-entropic behavior or phenomena.  Most are dismissed as the rantings of crackpots and lunatics.  This paper presents a coherent rational explanation, based on proven scientific principals, in support of these devices, and the phenomena observed.  It is also intended as a "how to" guide for current and future researchers in achieving optimal performance from their devices.  To those free thinking individuals, operating at the boundaries of knowledge, I dedicate this paper.

3.3.2

Conclusions:

That un-paired electron spins in paramagnetic materials will exhibit the characteristics of an inverted population (3.1.4).  That a population of un-paired electron spins can be made to interact with the zero point energy of electrodynamic space, thereby capturing thermal energy, and making it available for work (3.1.2, 3.1.3, 3.1.5, 3.2.2, 3.2.4).  That a cyclic heat engine, based on a working fluid, utilizing an inverted population of un-paired electron spins is possible (3.2.1, 3.2.2).  That said engine will exhibit anti-entropic behavior fully consistent with the principals of James C. Maxwell's Daemon (3.2.2, 3.2.4, 3.2.5).  That said engine is in fact, a perpetual motion device of the second type (3.2.2, 3.2.4, 3.2.5).